

The semi-interquartile range is 14 (28 ÷ 2) and the range is 43 (49-6).įor larger data sets, you can use the cumulative relative frequency distribution to help identify the quartiles or, even better, the basic statistics functions available in a spreadsheet or statistical software that give results more easily. The interquartile range will be Q3 - Q1, which gives 28 (43-15).
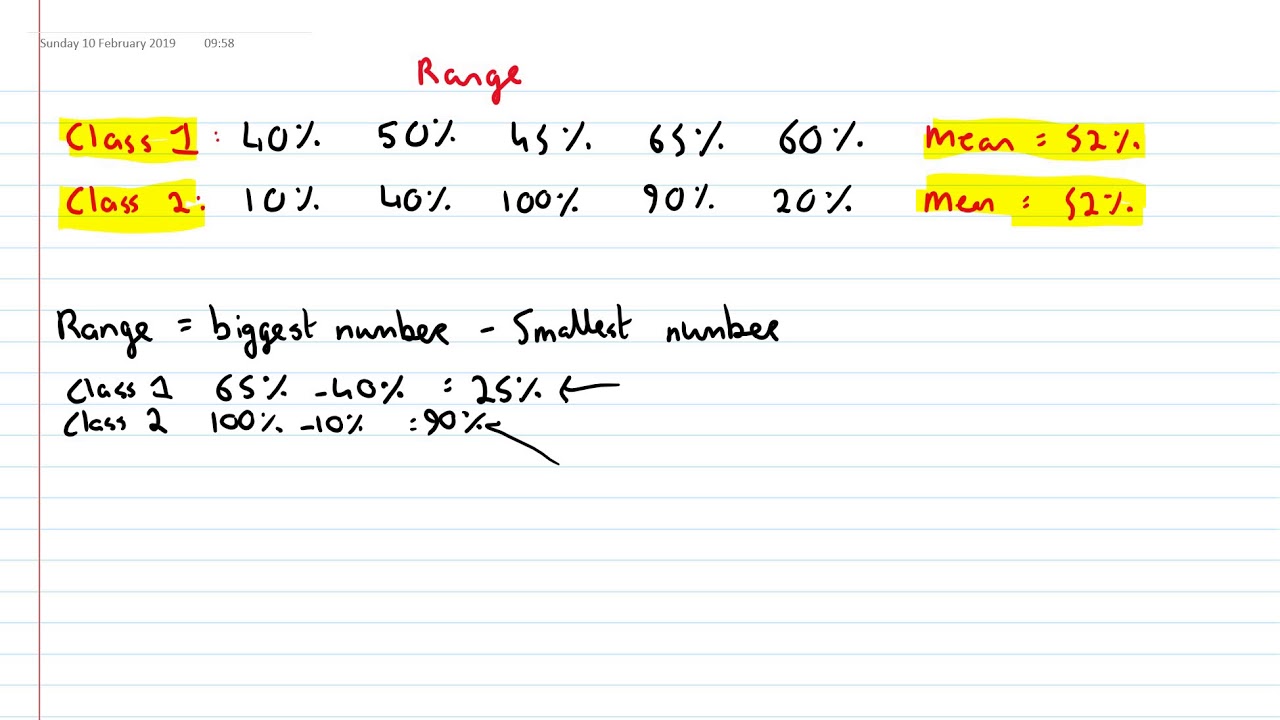
Once you have the quartiles, you can easily measure the spread. The rank of the upper quartile will be 6 + 3 = 9. The second half must also be split in two to find the value of the upper quartile. The lower quartile will be the point of rank (5 + 1) ÷ 2 = 3. Then you need to split the lower half of the data in two again to find the lower quartile. The rank of the median is 6, which means there are five points on each side. As we have seen in the section on the median, if the number of data points is an uneven value, the rank of the median will be Then you need to find the rank of the median to split the data set in two. The information is grouped by Rank (appearing as row headers), Value (appearing as column headers). This table displays the results of Rank of data points. Example 1 – Range and interquartile range of a data set When the data set is small, it is simple to identify the values of quartiles. The semi-interquartile range is half the interquartile range. The interquartile range is the difference between upper and lower quartiles. The median is considered the second quartile (Q2). The upper quartile, or third quartile (Q3), is the value under which 75% of data points are found when arranged in increasing order. The lower quartile, or first quartile (Q1), is the value under which 25% of data points are found when they are arranged in increasing order. To calculate these two measures, you need to know the values of the lower and upper quartiles. The interquartile range and semi-interquartile range give a better idea of the dispersion of data. It's used as a supplement to other measures, but it is rarely used as the sole measure of dispersion because it’s sensitive to extreme values. The range only takes into account these two values and ignore the data points between the two extremities of the distribution. The middle 50% of exam scores for Class B vary by 28 points.To calculate the range, you need to find the largest observed value of a variable (the maximum) and subtract the smallest observed value (the minimum). The middle 50% of exam scores for Class A vary by only 7.5 points.

Class A: IQR = Q3 – Q1 = 78.5 – 71 = 7.5Īs we observed earlier, Class A has less variability about its median.Here is the IQR for these two distributions: More specifically, the IQR tells us the range of the middle half of the data. The IQR is a measurement of the variability about the median. How are quartiles used to measure variability about the median? The interquartile range (IQR) is the distance between the first and third quartile marks. The 8 scores in Q3 vary by only 4 points. Compare this to the third quartile (Q3) for Class A: 25% of the scores in Class A are between 74.5 and 78.5.The eight scores in Q1 vary by 30 points. There is a lot of variability in this first quartile (Q1). For example, 25% of the scores in Class A are between 40 and 71.Notice: Some quartiles exhibit more variability in the data even though each quartile contains the same amount of data. Notice: The second quartile mark (Q2) is the median. The quartiles together with the minimum and maximum scores give the five-number summary: Class B has 20 scores, so each quartile contains five scores (20 ÷ 4 = 5).Class A has 32 scores, so each quartile contains eight scores (32 ÷ 4 = 8).Notice: For a data set, there is an equal amount of data in each quartile.


 0 kommentar(er)
0 kommentar(er)
